极限状态的平稳分布与周期
这篇文章概念和证明挺多,我把重要的概念和结论总结一下吧
闭集,不可约集
闭集
Definition 1: Closed Set 对于一个集合A,如果∀i∈A,j∉A,都有p(i,j)=0,那么称集合A是一个闭集。
不可约集
Definition 2: Irreducible Set 对于一个集合B,如果满足∀i,j∈B,都有i↔j,那么就称集合B是不可约的。
一个有用的结论
Lemma 1-1: Ex(N(y))=∑n=1∞pn(x,y)
Lemma 1:
如果x是一个常返状态,x→y,那么y也是一个常返状态。
Lemma 2:
在一个有限闭集中,至少有一个常返状态。
这里证明需要实分析的富比尼定理,有一步不太理解
极限下的平稳分布
随着时间的推移,不再受到随机过程的变化制约的分布
注意到
P(Xn=j)=∑iP(Xn−1=i)p(i,j)
定义
Definition 3: Stationary Distribution 如果qP=q,那么称q是一个平稳分布,用π表示。
没有额外的和约束,这个方程组并没有一个唯一解,因为矩阵不可能满秩
Theorem 1: 设转移矩阵P不可约,大小为k×k,那么方程解唯一,并且可以保证∀x,πx>0。
设Q=(P+I)/2,这里相当于我们构造了一条懒惰链,证明解的每个元素是恒正的(先证明同号再证明存在正元素)
不可约提供Q每个元素恒正的条件,同时保证从x到 y,一定存在一条经过k−1步的路径
懒惰链的作用文中没有细说,不过根据我的查阅,不可约集应该不能保证能返回自身,也就是懒惰链给自身循环加上0.5的概率,事实上加上多少都一样,目的是保证传递矩阵每个值都是正数
对闭集c,如果从c中任一状态出发经有限步转移到另一状态的概率都大于0,则称c为不可约闭集
最后我们来看一下唯一性。因为相当于有两个解,它们是正交的,满足同一个方程组。两个正交的解不可能都能够满足元素恒正
πP=π,事实上等价于这个式子
Lemma 3: πP=π ⇔∑y≠xπyp(y,x)=∑x≠yπxp(x,y)
从x点移出去的概率,等于从别的点移到x的概率
更加深层次的问题
平稳分布是否存在(注意,之前我们的定理并没有讨论存在性)?状态多久会被访问一次?
如果x所到达的状态y是一个瞬时状态,这没什么好说的,因为这个时候,我们根据瞬时状态的性质,可以得到
∀x,Ex(N(y))=∑n=1∞pn(x,y)<∞
潜在意思是说,pn(x,y)→0,∀x,换句话说,如果y是瞬时的,那么极限状态下,从哪儿到达y的概率都会趋于0。
很多时候平稳状态不存在,但是每一个状态隔几轮就会被访问一次。这就引入了周期性(periodicity)的概念。
Definition 4: Period 定义状态的周期为集合Ix={n≥1:pn(x,x)>0}元素的最大公约数。
直观来看,这个集合就是x有概率返回到x,要经过的转移次数的集合。
关于集合Ix有一个很有意思的引理。
Lemma 4: 若i,j∈Ix,那么i+j∈Ix
用抽代的话来说,就是集合对加法运算封闭
非周期(aperiodic)状态的情况,也就是所有状态的周期为1的情况。
Proposition 1: 如果状态x的周期为1,那么存在n0∈N+,使得如果n≥n0,那么n∈Ix。
这里的证明比较有意思,从K,K+1构造任意长度的连续序列,反证法证明不存在最大上限,再证明K,K+1可以通过裴蜀(Bezout)定理找到
裴蜀(Bezout)定理:若a,b是整数,且[gcd](a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
下一个性质也比较有趣。
Proposition 2: 如果x↔y,那么x,y具有相同的周期。
这是用对称放缩证明
一些特殊的马尔科夫链
双随机链(doubly stochastic chains)。
Definition 4: Doubly Stochastic Chains 如果一条马尔科夫链的转移矩阵满足∑xp(x,y)=1,那么称它为双随机的。
如果转移矩阵满足这个,事实上我们可以非常容易的找到它的平稳分布:假如它的大小是k×k,那么它的平稳分布就是πx=1/k
细致平衡条件(detailed balance condition)
Definition 5: Detailed Balance Condition 如果分布满足πxp(x,y)=πyp(y,x),那么称它满足细致平衡条件。
任意两个点之间相互转移的概率相等,很明显是一个比平稳更强的条件(平稳的含义就是所有从x离开的概率等于回到x的概率)。更具体地说,分布满足这个条件,就一定是平稳分布。
这个条件可以解决醉汉问题:
Problem 2: 考虑一个无向图,一个醉汉会在某个点,按照相同的概率沿着它的邻边走下一步。描述出这个问题的转移矩阵,并分析最后的平稳分布。
通过细致平衡条件来看是否可以推出平稳分布。首先可以得到
πup(u,v)=πvp(v,u)
那么代入上面的式子,我们就可以得到
πu / πv=d(u) / d(v)
所以我们再标准化一下,其实不难得到πu=d(u) / ∑ud(u)。换句话说,醉汉最终更有可能去向邻边多的区域。我们也可以合理推断,对于一个毫无自主意识的醉汉来说,它最有可能出现在路口多的位置
逆马尔科夫链(reversible Markov chain)
只是把原先的马尔科夫链倒过来看所产生的结果,这样得到的一条随机过程仍然是一条马尔科夫链。
Proposition 3: 考虑{Xn}为一条马尔科夫链,具备平稳分布π,且假设起始分布就是平稳分布。设Ym=Xn−m,0≤m≤n,那么Ym依然是一个马尔科夫链,并且有 p^(i,j)=P(Ym+1=j|Ym=i)=π(j)p(j,i) / π(i)
用图来描述大概就是这样的。
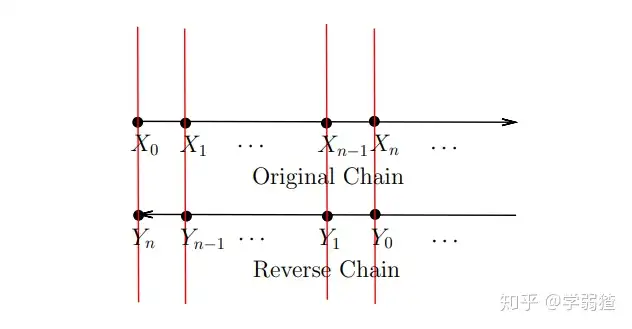
如果{Xn}满足细致平衡条件,那么就可以得到p^(i,j)=p(i,j)。相当于这一条马尔科夫链,正着走反着走,它的转移矩阵是不变的。