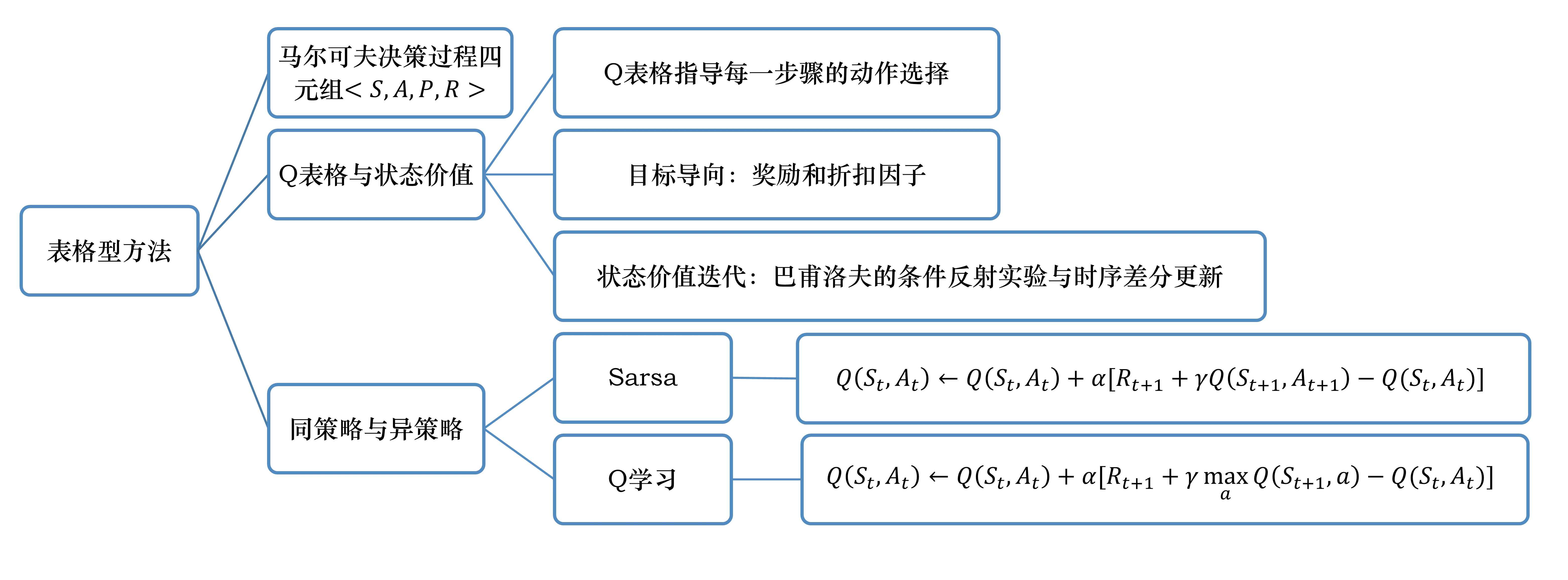
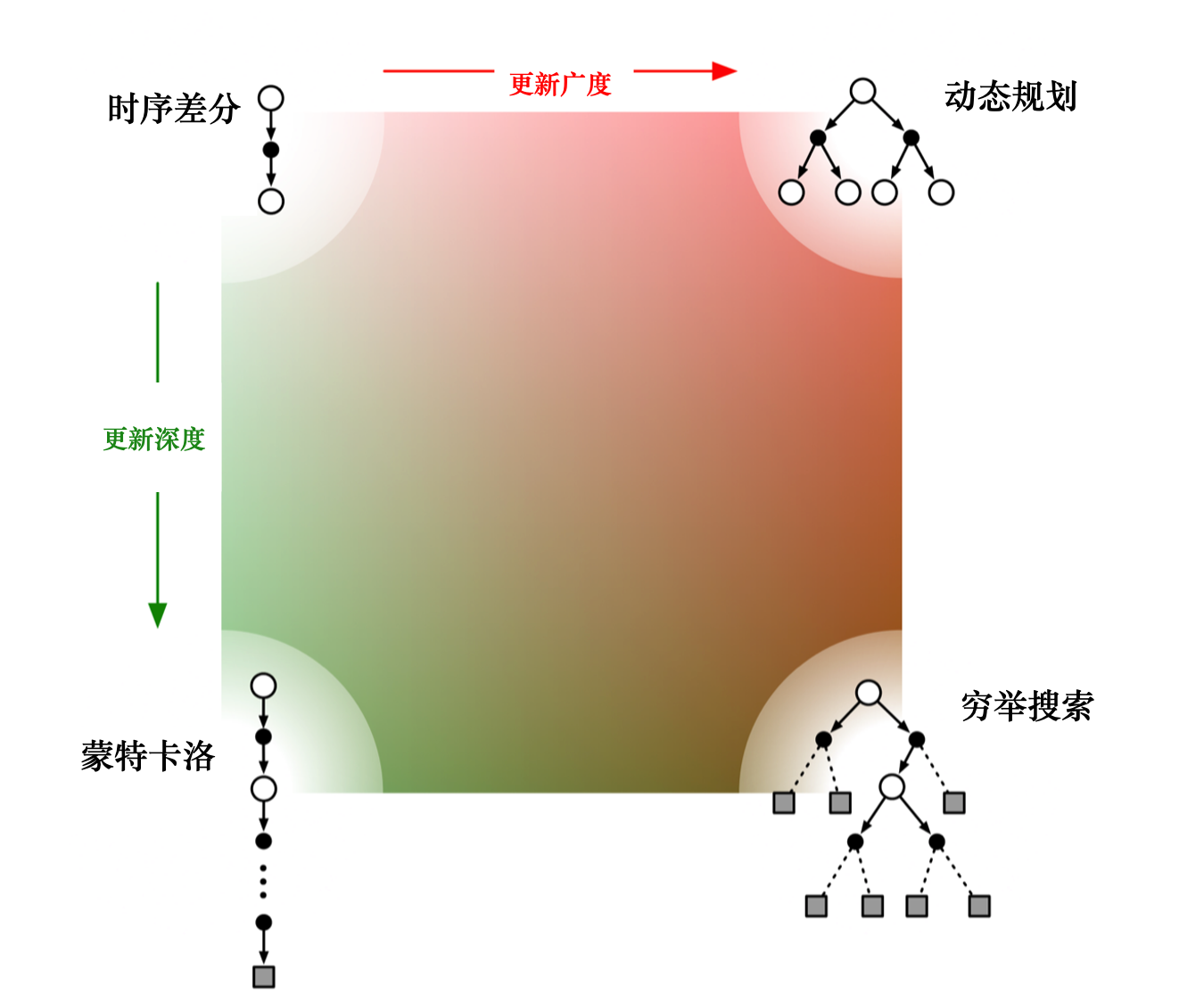
动态规划方法、蒙特卡洛方法以及时序差分方法的自举和采样
自举是指更新时使用了估计。蒙特卡洛方法没有使用自举,因为它根据实际的回报进行更新。 动态规划方法和时序差分方法使用了自举。
采样是指更新时通过采样得到一个期望。 蒙特卡洛方法是纯采样的方法。 动态规划方法没有使用采样,它是直接用贝尔曼期望方程来更新状态价值的。 时序差分方法使用了采样。时序差分目标由两部分组成,一部分是采样,一部分是自举。
动态规划方法直接计算期望,它把所有相关的状态都进行加和
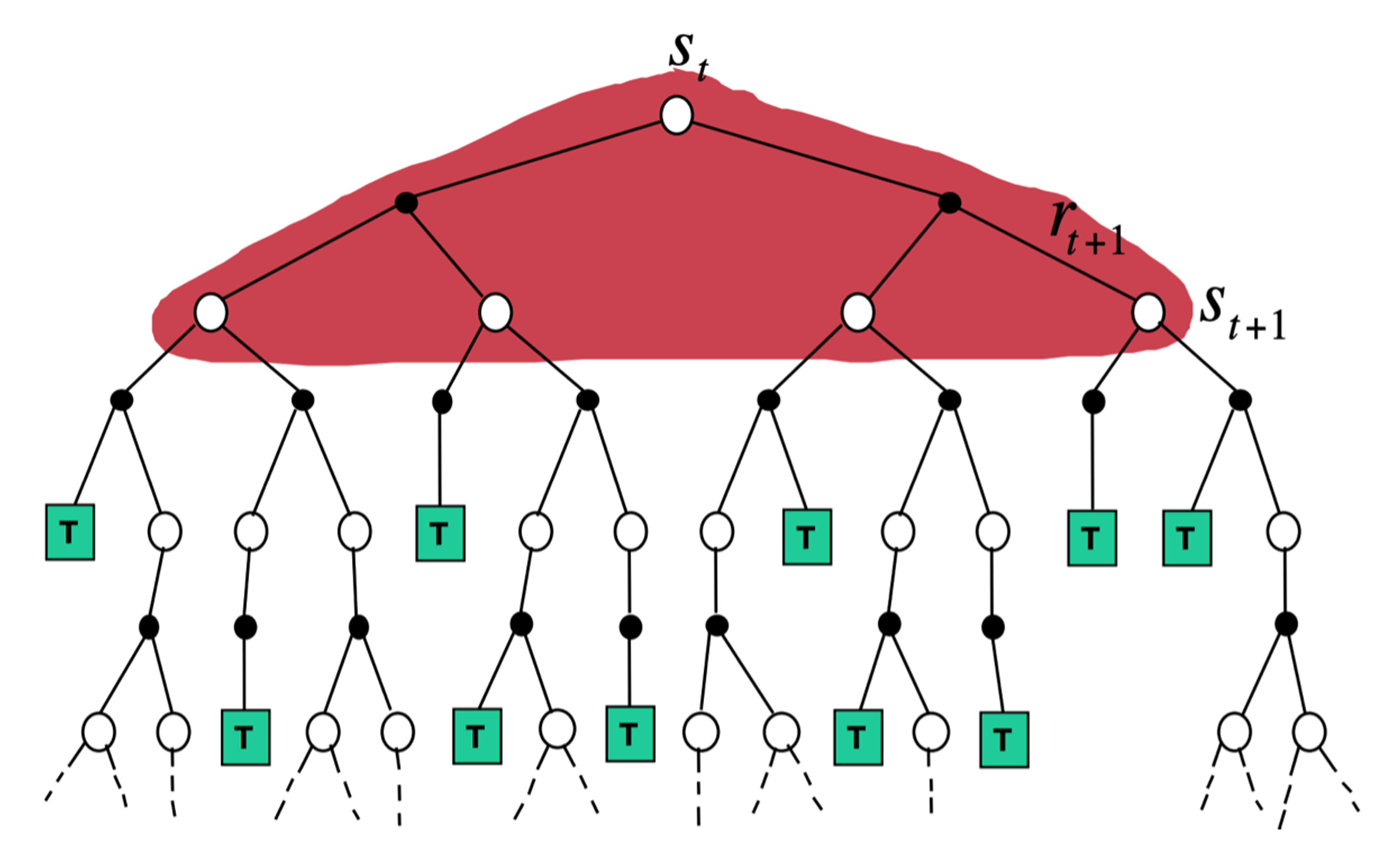
蒙特卡洛方法在当前状态下,采取一条支路,在这条路径上进行更新,更新这条路径上的所有状态
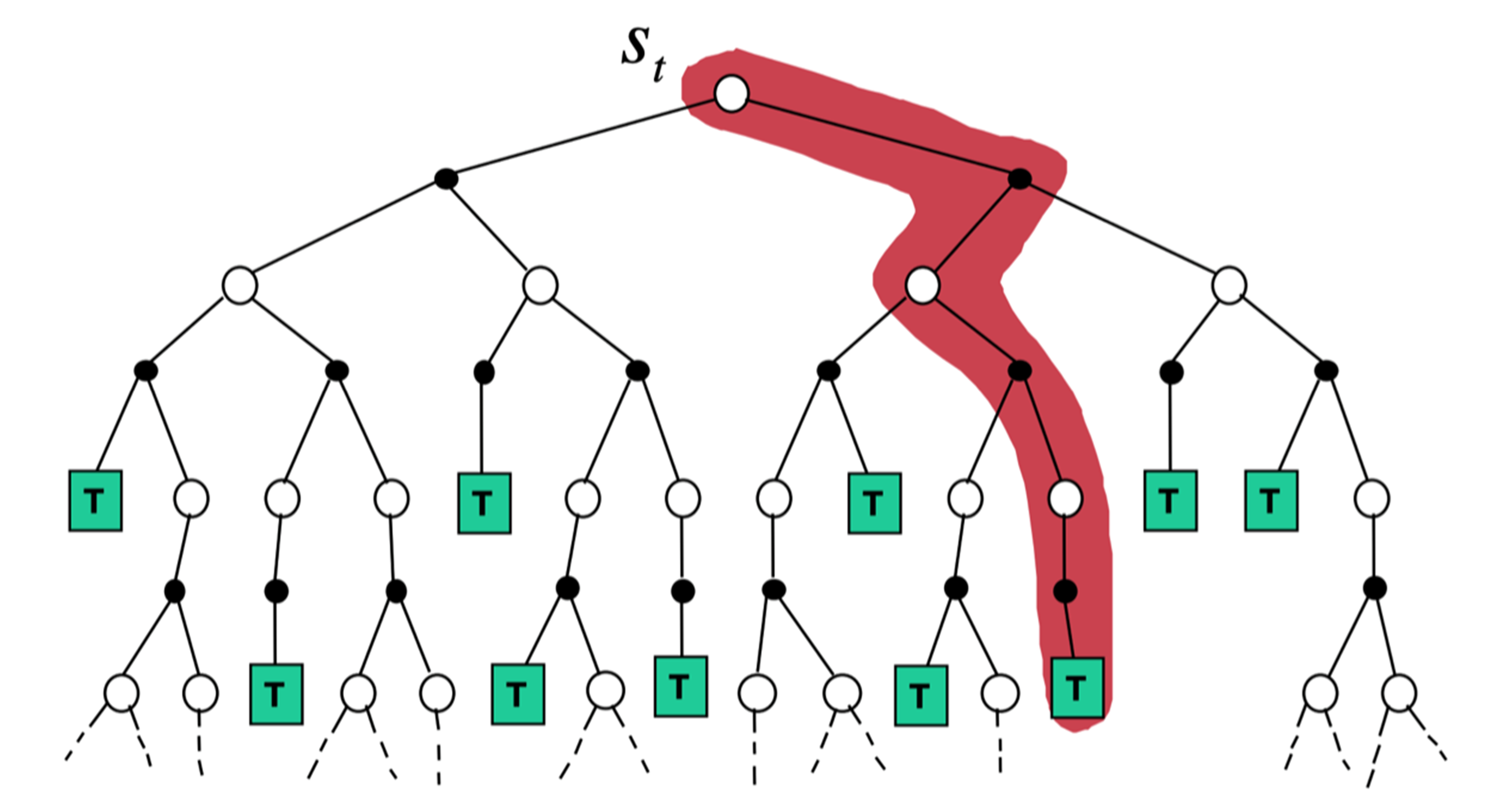
时序差分从当前状态开始,往前走了一步,关注的是非常局部的步骤
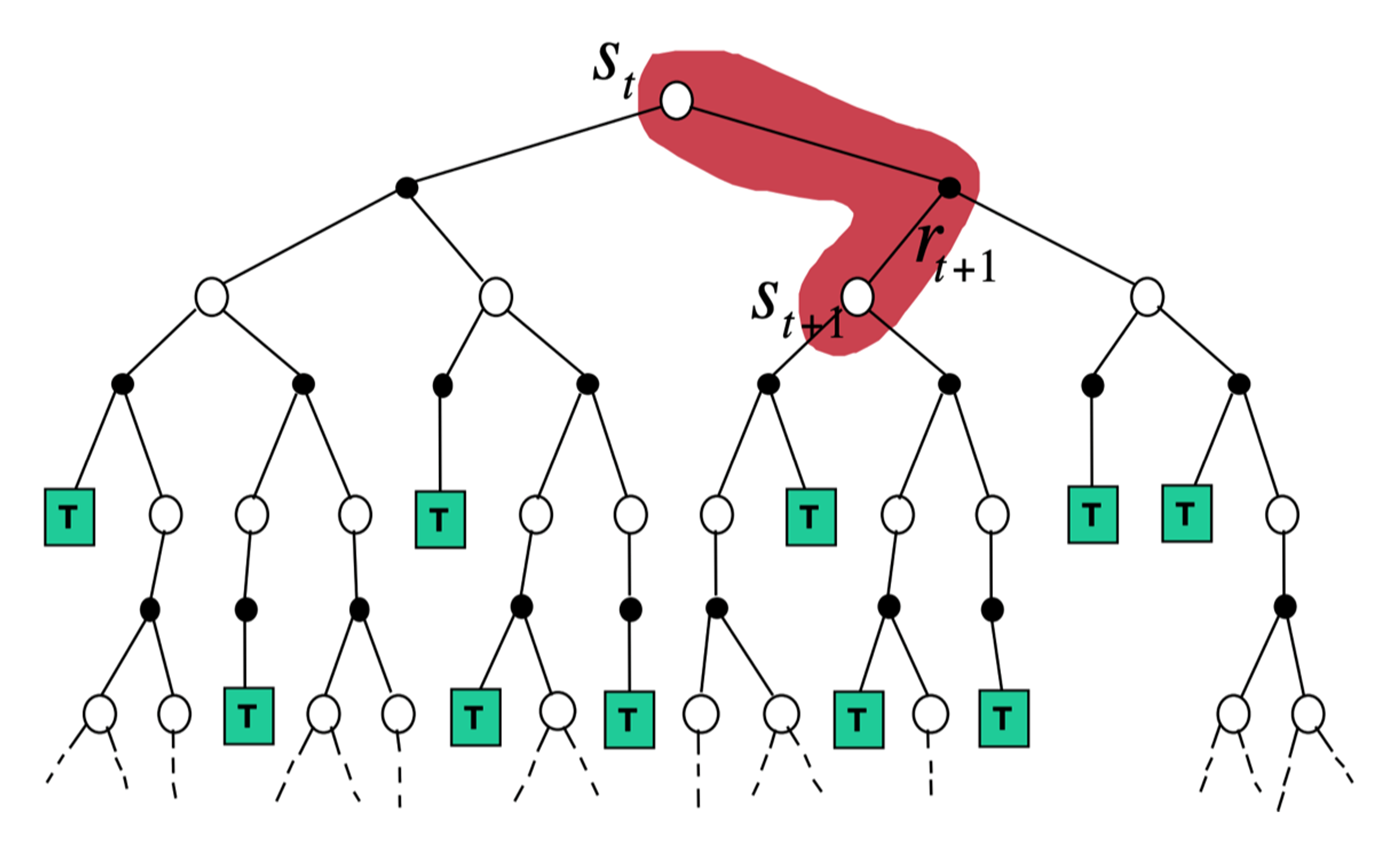
- 如果 时序差分方法需要更广度的更新,就变成了 动态规划方法(因为动态规划方法是把所有状态都考虑进去来进行更新)。如果时序差分方法需要更深度的更新,就变成了蒙特卡洛方法
当我们不知道奖励函数和状态转移时,如何进行策略的优化?针对上述情况,我们引入了广义的策略迭代的方法。 我们对策略评估部分进行修改,使用蒙特卡洛的方法代替动态规划的方法估计 Q 函数。我们首先进行策略评估,使用蒙特卡洛方法来估计策略 ,然后进行策略更新,即得到 Q 函数后,我们就可以通过贪心的方法去改进它
为了确保蒙特卡洛方法能够有足够的探索,我们使用了ε-贪心(ε-greedy)探索。ε-贪心是指我们有1−ε 的概率会按照 Q函数来决定动作,通常ε 就设一个很小的值,1−ε 可能是 0.9,也就是 0.9 的概率会按照Q函数来决定动作,但是我们有 0.1 的概率是随机的。

接下来随着训练的次数越来越多,我们已经比较确定哪一个动作是比较好的,就会减少探索,把ε的值变小。主要根据Q函数来决定动作,比较少随机决定动作,这就是ε-贪心。
Sarsa:同策略时序差分控制
时序差分方法是给定一个策略,然后我们去估计它的价值函数。接着我们要考虑怎么使用时序差分方法的框架来估计Q函数,也就是 Sarsa 算法。
Sarsa 所做出的改变很简单,它将原本时序差分方法更新V 的过程,变成了更新 Q
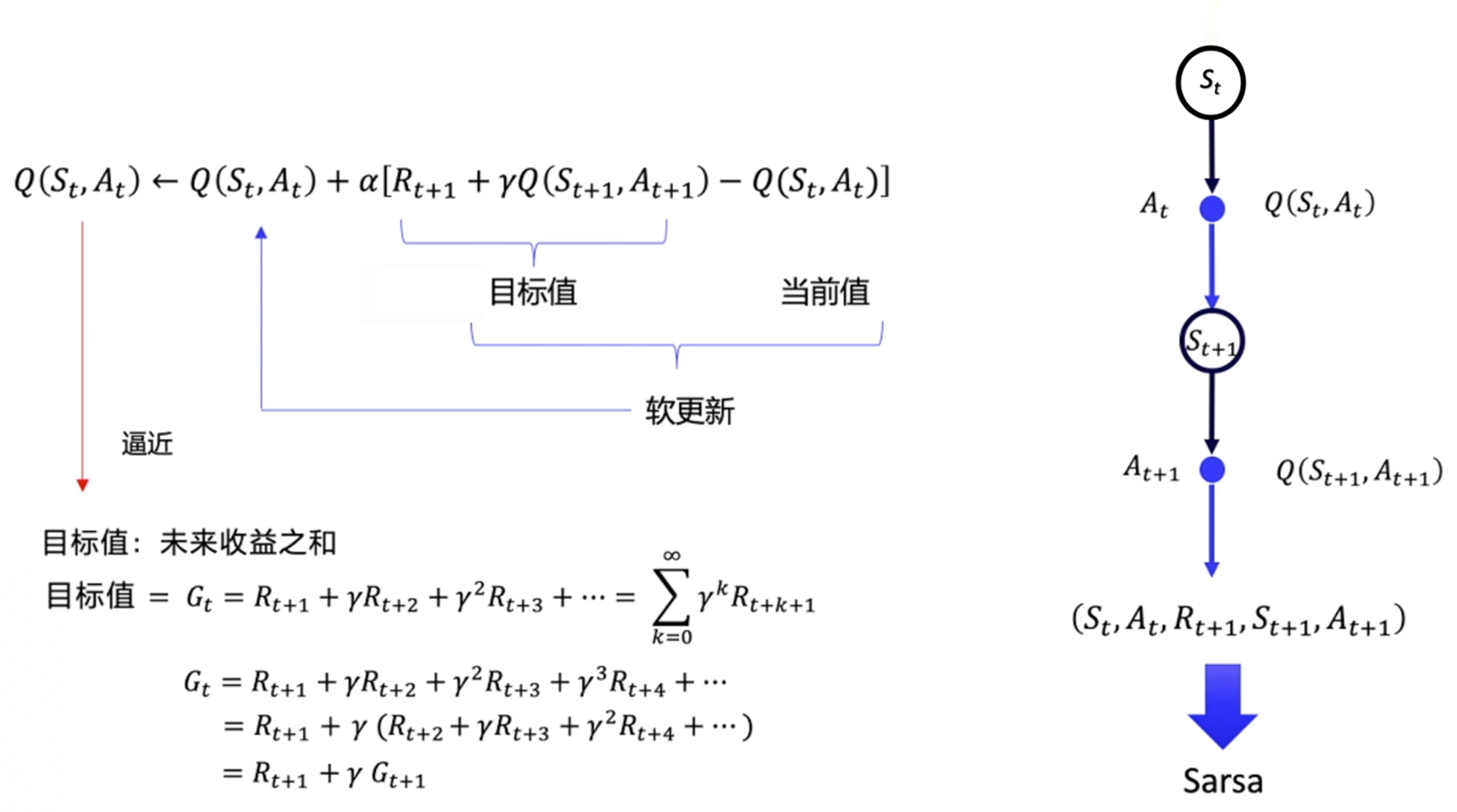
我们用软更新的方式来逼近。软更新的方式就是每次我们只更新一点点,α 类似于学习率。
Q学习:异策略时序差分控制
Sarsa 是一种同策略(on-policy)算法,它优化的是它实际执行的策略,它直接用下一步会执行的动作去优化 Q 表格。
Q学习是一种异策略(off-policy)算法。如图 3.31 所示,异策略在学习的过程中,有两种不同的策略:目标策略(target policy)和行为策略(behavior policy)。
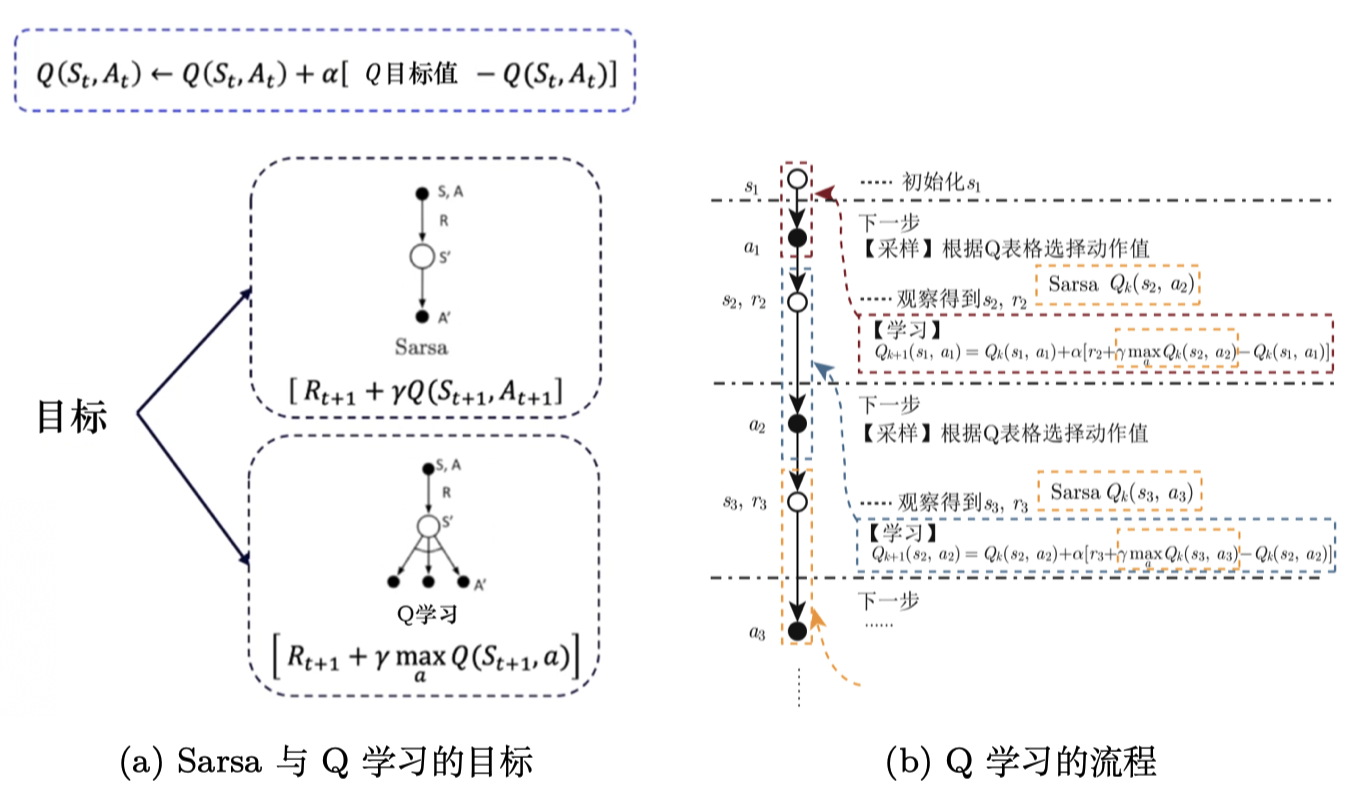
总结一下同策略和异策略的区别
Sarsa 是一个典型的同策略算法,它只用了一个策略 π,它不仅使用策略 π学习,还使用策略 π与环境交互产生经验。 如果策略采用 ε-贪心算法,它需要兼顾探索,为了兼顾探索和利用,它训练的时候会显得有点“胆小”。
Q学习是一个典型的异策略算法,它有两种策略————目标策略和行为策略,它分离了目标策略与行为策略。Q学习可以大胆地用行为策略探索得到的经验轨迹来优化目标策略,从而更有可能探索到最佳策略。行为策略可以采用 ε-贪心 算法,但目标策略采用的是贪心算法,它直接根据行为策略采集到的数据来采用最佳策略,所以 Q学习 不需要兼顾探索。
Q学习是一个非常激进的方法,它希望每一步都获得最大的利益;Sarsa 则相对较为保守,它会选择一条相对安全的迭代路线