免模型控制
把策略迭代进行广义的推广,使它能够兼容蒙特卡洛和时序差分的方法,即带有蒙特卡洛方法和时序差分方法的广义策略迭代(generalized policy iteration,GPI)
策略迭代由两个步骤组成。第一,我们根据给定的当前策略 π 来估计价值函数;第二,得到估计的价值函数后,我们通过贪心的方法来改进策略
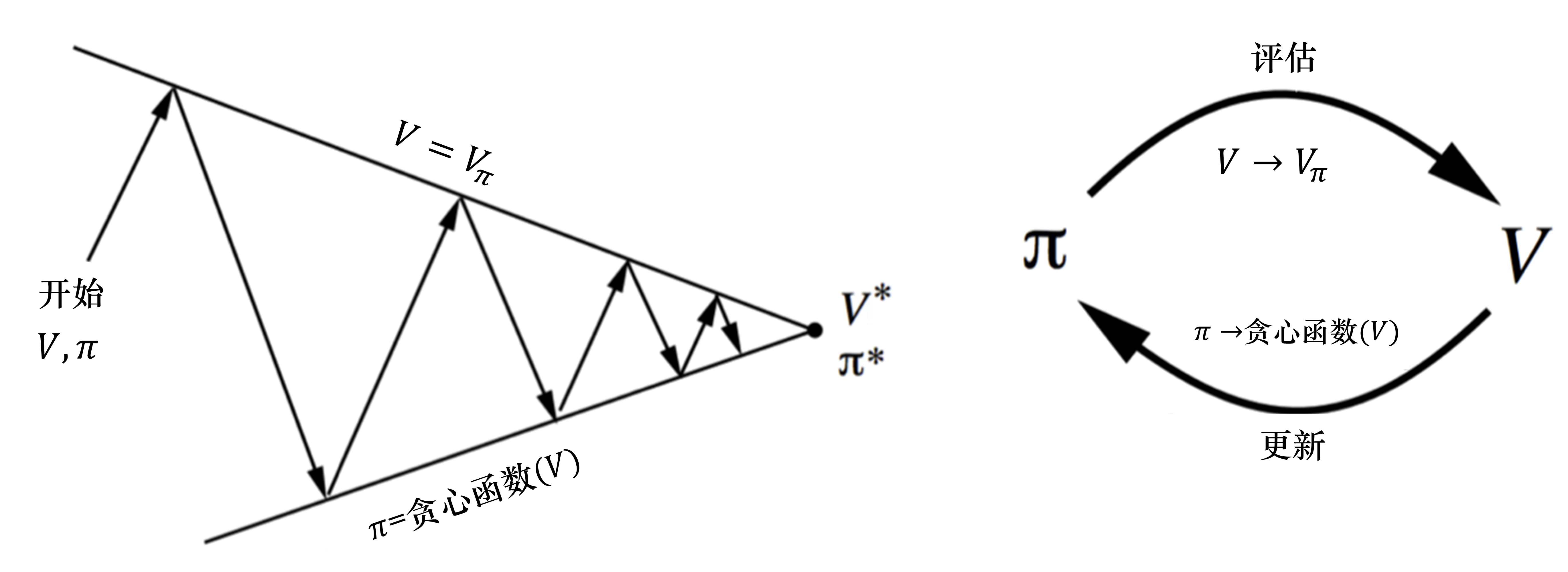
这里有一个问题:当我们不知道奖励函数和状态转移时,如何进行策略的优化?
针对上述情况,我们引入了广义的策略迭代的方法。 我们对策略评估部分进行修改,使用蒙特卡洛的方法代替动态规划的方法估计 Q 函数。我们首先进行策略评估,使用蒙特卡洛方法来估计策略Q=Qπ,然后进行策略更新,即得到 Q 函数后,我们就可以通过贪心的方法去改进它
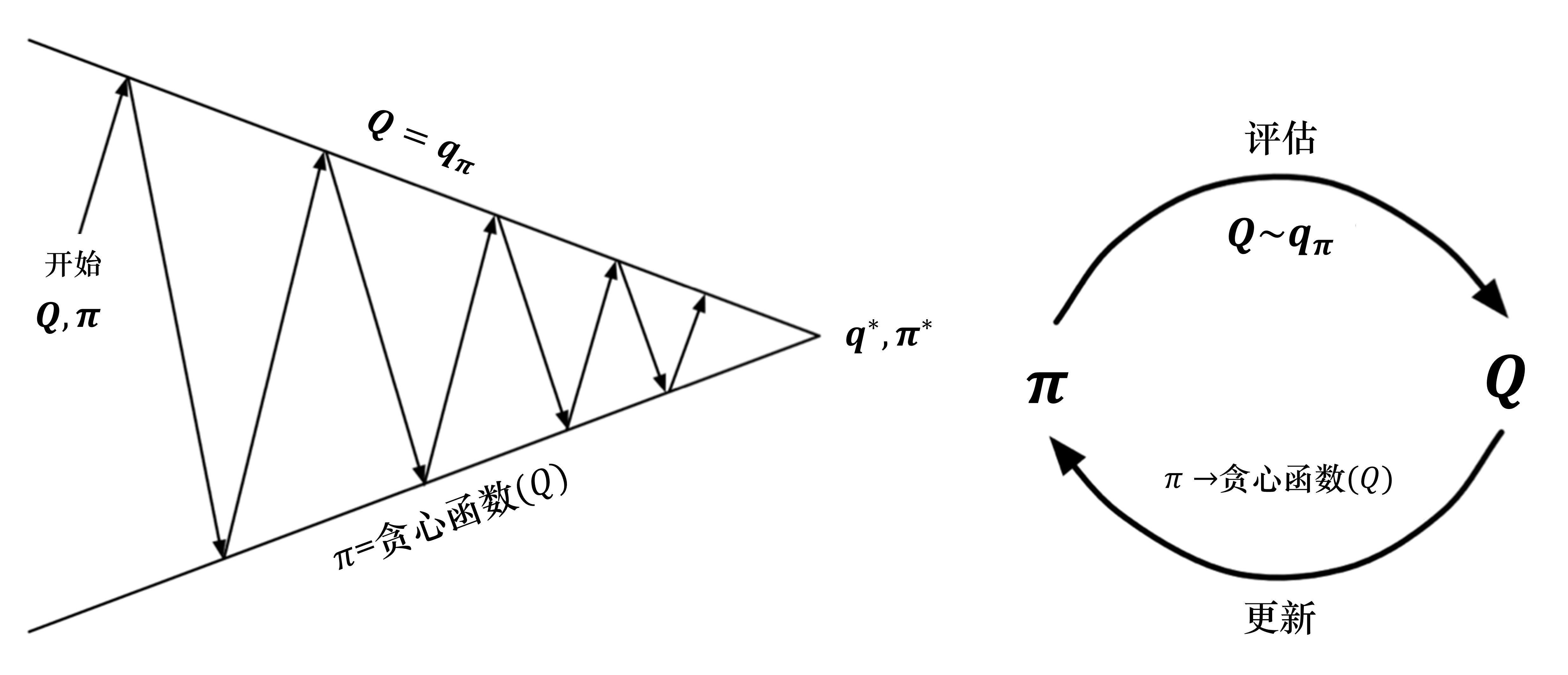
一个保证策略迭代收敛的假设是回合有探索性开始(exploring start)。 假设每一个回合都有一个探索性开始,探索性开始保证所有的状态和动作都在无限步的执行后能被采样到,这样才能很好地进行估计。 算法通过蒙特卡洛方法产生很多轨迹,每条轨迹都可以算出它的价值。然后,我们可以通过平均的方法去估计 Q 函数。Q 函数可以看成一个Q表格,我们通过采样的方法把表格的每个单元的值都填上,然后使用策略改进来选取更好的策略。 如何用蒙特卡洛方法来填 Q 表格是这个算法的核心。
以上是免模型控制的一些补充
总的来说,免模型预测有蒙特卡洛策略评估,时序差分和动态规划三种方法,免模型控制有Sarsa和Q学习两种时序差分控制,Sarsa同策略,Q异策略
基于价值的方法中动作-价值对的估计值最终会收敛(通常是不同的数,可以转化为0~1的概率),因此通常会获得一个确定的策略;基于策略的方法不会收敛到一个确定的值,另外他们会趋向于生成最佳随机策略。如果最佳策略是确定的,那么最优动作对应的值函数的值将远大于次优动作对应的值函数的值,值函数的大小代表概率的大小。
蒙特卡洛方法是无偏估计,时序差分方法是有偏估计;蒙特卡洛方法的方差较大,时序差分方法的方差较小,原因在于时序差分方法中使用了自举,实现了基于平滑的效果,导致估计的价值函数的方差更小。