策略梯度

策略一般记作 π。假设我们使用深度学习来做强化学习，策略就是一个网络。网络里面有一些参数，我们用 θ 来代表 π 的参数。

也许我们觉得游戏的画面是前后相关的，所以应该让策略去看从游戏开始到当前这个时间点之间所有画面的总和。因此我们可能会觉得要用到循环神经网络（recurrent neural network，RNN）来处理它，不过这样会比较难处理。我们可以用向量或矩阵来表示智能体的观测，并将观测输入策略网络，策略网络就会输出智能体要采取的动作。
通常我们无法控制环境，因为环境是设定好的。我们能控制的是Pθ(αt|St) 给定一个 S，演员要采取的 α 取决于演员的参数 θ， 所以智能体的动作是演员可以控制的。演员的动作不同，每个同样的轨迹就有不同的出现的概率。
首先我们要收集很多s与a的对（pair），还要知道这些s与a在与环境交互的时候，会得到多少奖励。 这些数据怎么收集呢？我们要用参数为θ的智能体与环境交互， 也就是拿已经训练好的智能体先与环境交互，交互完以后，就可以得到大量游戏的数据

——————–

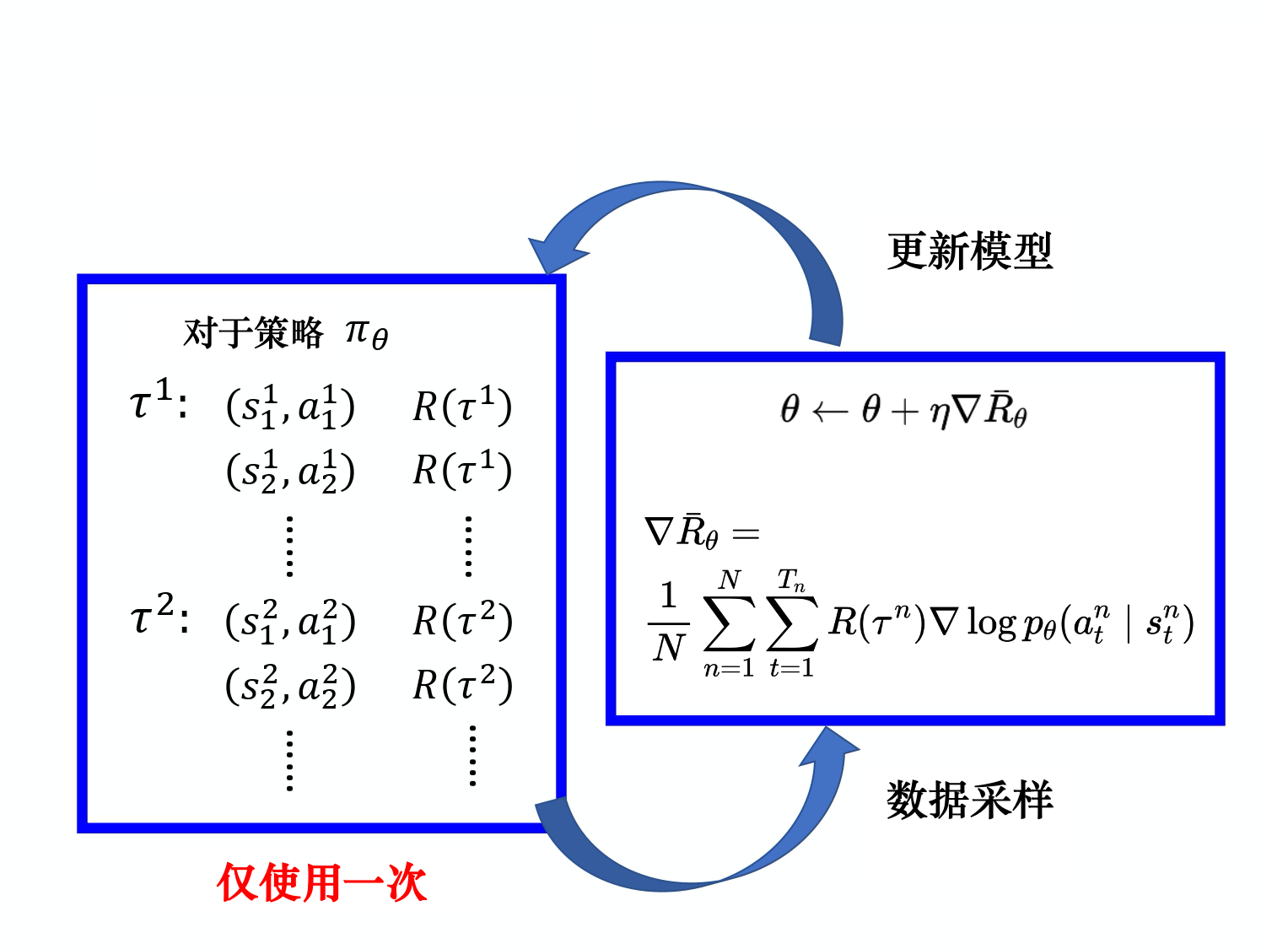
策略梯度实现技巧

1.添加基线

使得奖励有正有负，再用归一化更符合实际

2.分配合适的分数

一个做法是计算某个状态-动作对的奖励的时候，不把整场游戏得到的奖励全部加起来，只计算从这个动作执行以后得到的奖励。因为这场游戏在执行这个动作之前发生的事情是与执行这个动作是没有关系的，所以在执行这个动作之前得到的奖励都不能算是这个动作的贡献。
把未来的奖励做一个折扣，因为虽然在某一时刻，执行某一个动作，会影响接下来所有的结果（有可能在某一时刻执行的动作，接下来得到的奖励都是这个动作的功劳），但在一般的情况下，时间拖得越长，该动作的影响力就越小。
优势函数在意的不是绝对的好，而是相对的好，即相对优势（relative advantage）。因为在优势函数中，我们会减去一个基线 b，所以这个动作是相对的好，不是绝对的好。Aθ 通常可以由一个网络估计出来，这个网络称为评论员（critic）。
—————–

REINFORCE:蒙特卡洛策略梯度

蒙特卡洛方法可以理解为算法完成一个回合之后，再利用这个回合的数据去学习，做一次更新。
因为我们已经获得了整个回合的数据，所以也能够获得每一个步骤的奖励，我们可以很方便地计算每个步骤的未来总奖励，即回报Gt 相比蒙特卡洛方法一个回合更新一次，时序差分方法是每个步骤更新一次，即每走一步，更新一次

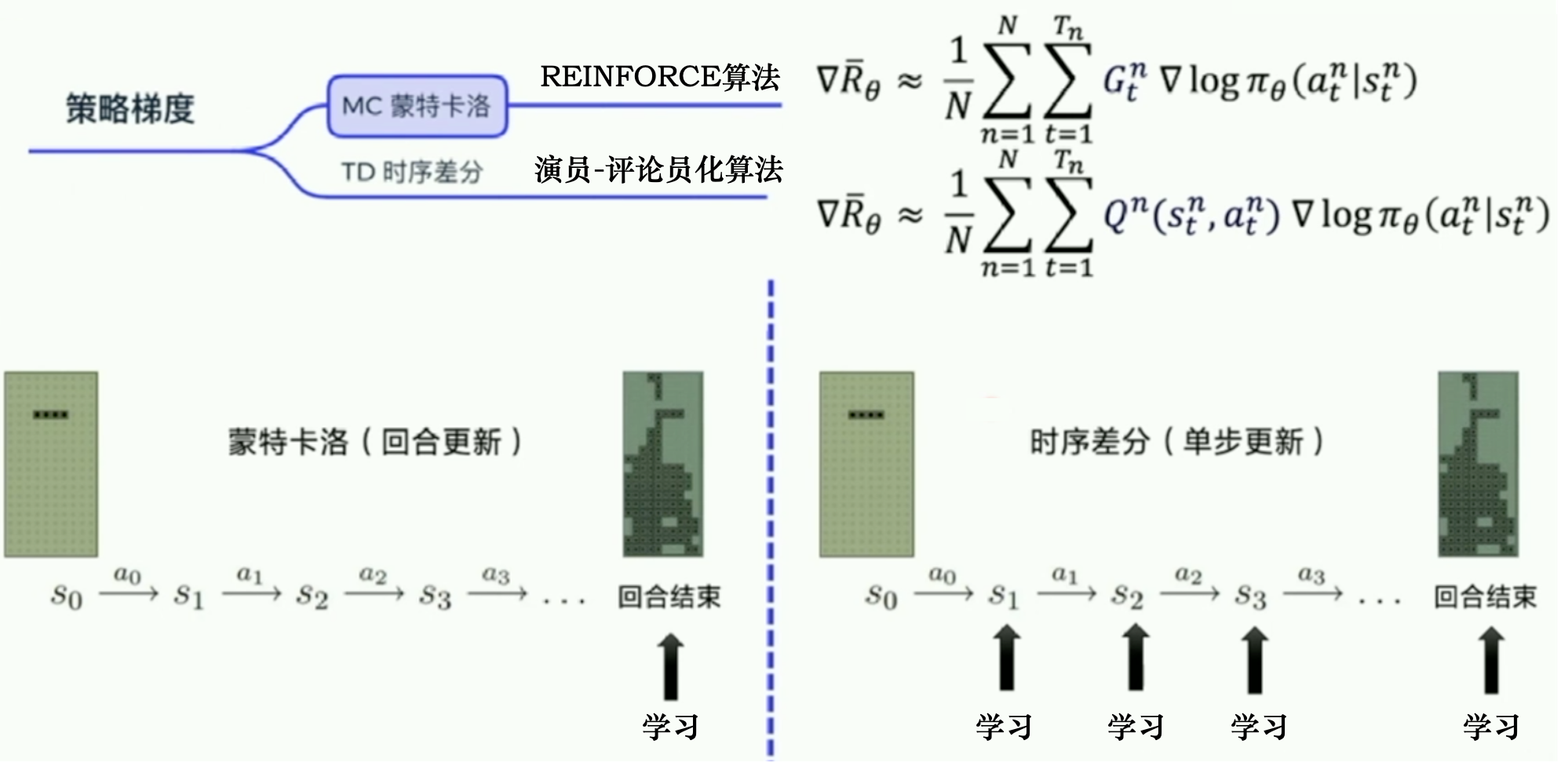
神经网络输出每个动作对应概率值，然后获取实际动作at，将动作转成独热向量与log相乘