深度Q网络
传统的强化学习算法会使用表格的形式存储状态价值函数V或动作价值函数Q,但是这样的方法存在很大的局限性。例如,现实中的强化学习任务所面临的状态空间往往是连续的,存在无穷多个状态,在这种情况下,就不能再使用表格对价值函数进行存储。
价值函数近似(value function approximation)利用函数直接拟合状态价值函数或动作价值函数,降低了对存储空间的要求,有效地解决了这个问题。
深度Q网络(deep Q-network,DQN)是指基于深度学习的Q学习算法,主要结合了价值函数近似与神经网络技术,并采用目标网络和经历回放的方法进行网络的训练。
状态价值函数
深度Q网络 是基于价值的算法,在基于价值的算法里面,我们学习的不是策略,而是评论员(critic)
蒙特卡洛方法最大的问题就是方差很大。游戏本身是有随机性的,Ga(Sa接下来的累计奖励)可以看作一个随机变量
所有步骤累积的方差 Var[kX]=k^2Var[X]
动作价值函数
假设我们有一个Q函数和某一个策略 π,根据策略 π 学习出策略 π 的 Q 函数,接下来可以找到一个新的策略 π′ ,它会比 π 要好。我们用 π′取代 π,再去学习它的 Q 函数,得到新的Q函数以后,再去寻找一个更好的策略。这样一直循环下去,策略就会越来越好。
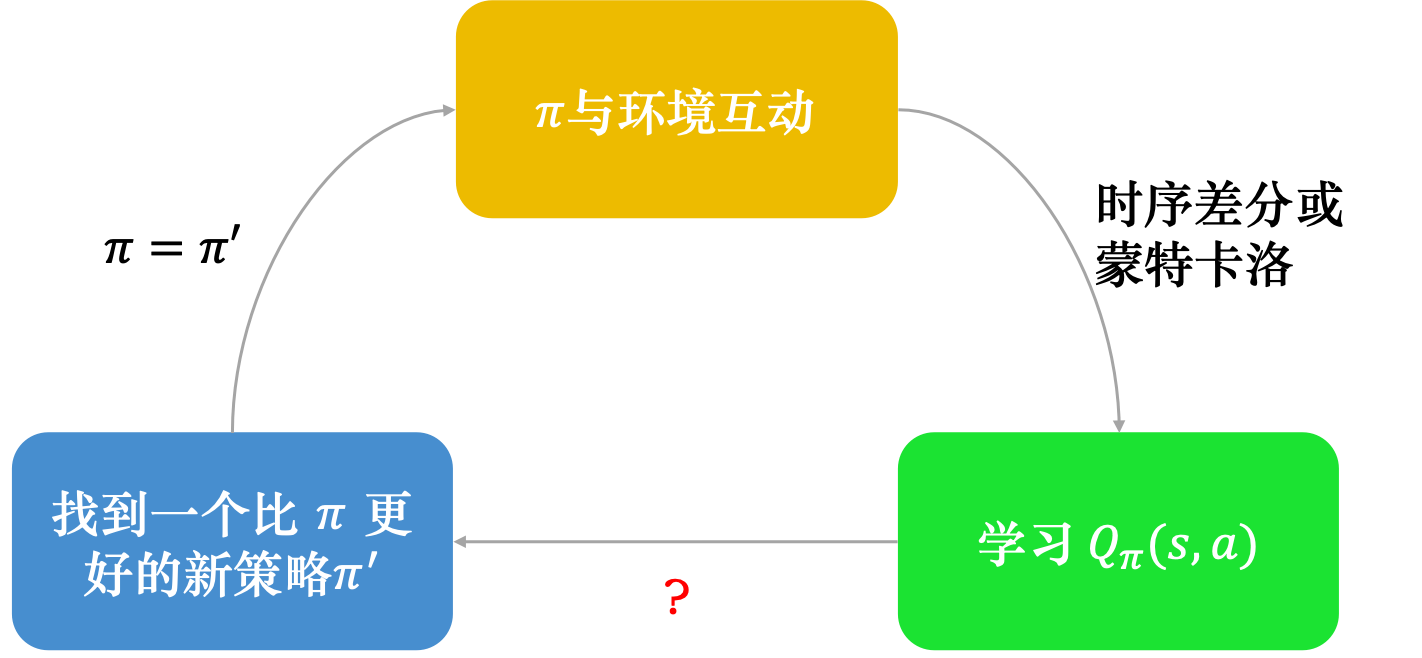
注意,给定状态 s 和策略 π 并不一定会采取动作 a。给定某一个状态 s 强制采取动作 a,用 π 继续交互得到的期望奖励,这才是Q函数的定义。
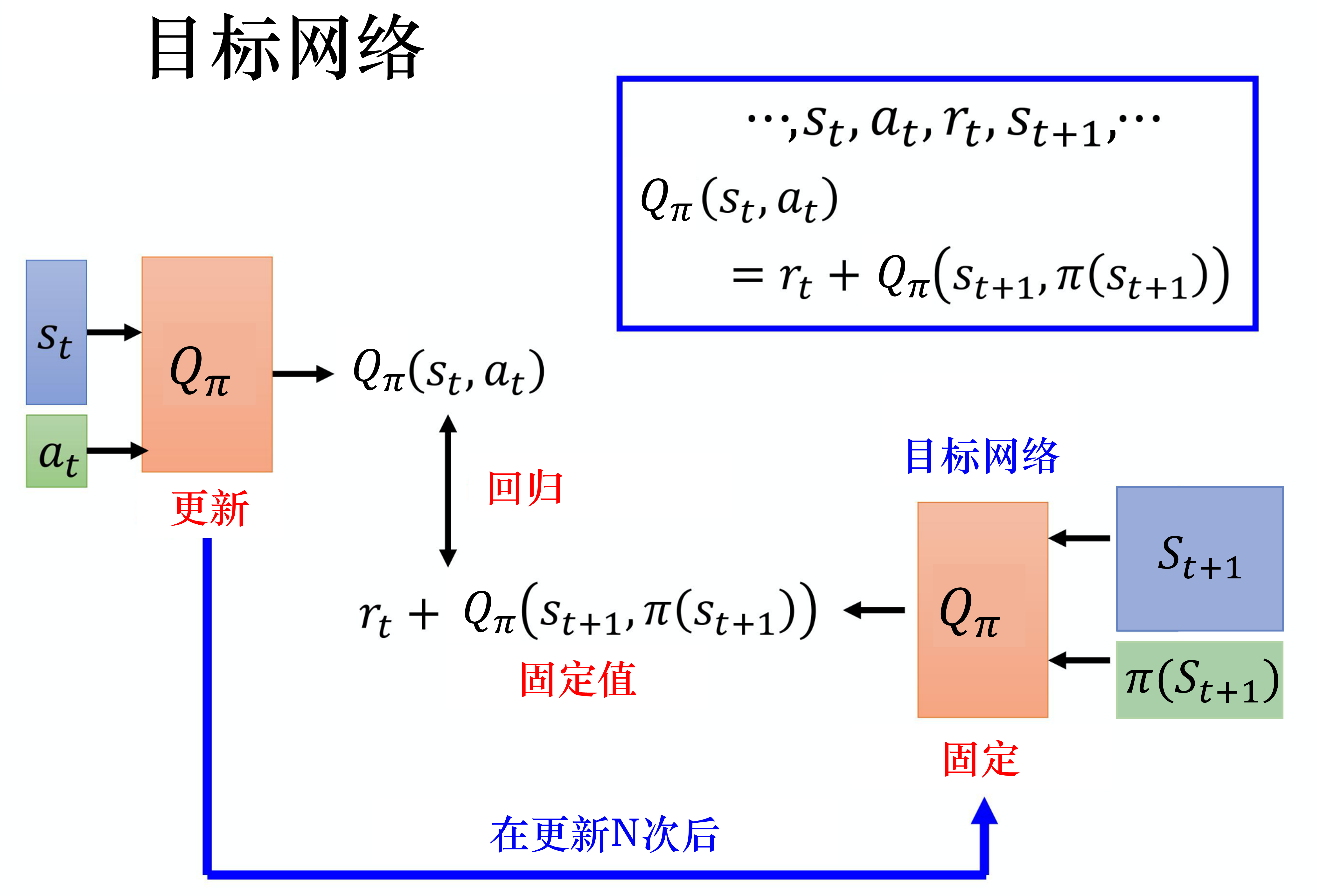
目标网络
把其中一个 Q 网络固定住。在训练的时候,只更新左边的 Q 网络的参数,而右边的 Q 网络的参数会被固定。因为右边的 Q 网络负责产生目标,所以被称为目标网络。
在实现的时候,我们会把左边的 Q 网络更新多次,再用更新过的 Q 网络替换目标网络。
就好像我们本来在做一个回归问题,训练后把这个回归问题的损失降下去以后,接下来我们把左边网络的参数复制到右边网络,目标值就变了,接下来就要重新训练。
探索
探索-利用窘境(exploration-exploitation dilemma)问题,有两个方法可以解决这个问题:ε-贪心和玻尔兹曼探索(Boltzmann exploration)。
通常将 ε 设为一个很小的值, 1−1−ε 可能是 0.9,也就是 0.9 的概率会按照Q函数来决定动作,但是我们有 0.1 的概率是随机的。通常在实现上 ε 会随着时间递减。
玻尔兹曼探索中,T>0 称为温度系数。如果 T 很大,所有动作几乎以等概率选择(探索);如果 T 很小,Q值大的动作更容易被选中(利用);如果 T 趋于0,我们就只选择最优动作。
经验回放
经验回放(experience replay)。经验回放会构建一个回放缓冲区(replay buffer),回放缓冲区又被称为回放内存(replay memory)。
回放缓冲区里面的经验可能来自不同的策略
在每次迭代里面,从回放缓冲区中随机挑一个批量(batch)出来,即与一般的网络训练一样,从训练集里面挑一个批量出来。我们采样该批量出来,里面有一些经验,我们根据这些经验去更新Q函数。这与时序差分学习要有一个目标网络是一样的。我们采样一个批量的数据,得到一些经验,再去更新 Q 函数。
实际上存储在回放缓冲区里面的这些经验不是通通来自于 π,有些是过去其他的策略所留下来的经验
第一个好处是,在进行强化学习的时候, 往往最花时间的步骤是与环境交互,训练网络反而是比较快的。因为我们用 GPU 训练其实很快,真正花时间的往往是与环境交互。用回放缓冲区可以减少与环境交互的次数
第二个好处是,在训练网络的时候,其实我们希望一个批量里面的数据越多样(diverse)越好。如果批量里面的数据都是同样性质的,我们训练下去,训练结果是容易不好的。
深度Q网络

主要的不同点在于:深度Q网络 将Q学习与深度学习结合,用深度网络来近似动作价值函数,而 Q学习 则是采用表格存储;深度Q网络采用了经验回放的训练方法,从历史数据中随机采样,而Q学习直接采用下一个状态的数据进行学习。