双深度网络(double DQN,DDQN)
在实际上,Q 值往往是被高估的。
我们会得到在某一个状态采取某一个动作的累积奖励是多少。预估出来的值远比真实值大,且大很多,在每一个游戏中都是这样。所以DDQN的方法可以让预估值与真实值比较接近。
智能体总是会选那个 Q 值被高估的动作,总是会选奖励被高估的动作的Q值当作最大的结果去加上 rt当作目标,所以目标值总是太大。
在DDQN里面,选动作的Q函数与计算值的Q函数不是同一个。
假设我们有两个Q函数————Q和Q`,如果 Q 高估了它选出来的动作 a,只要 Q′没有高估动作 a 的值,算出来的就还是正常的值。假设 Q′高估了某一个动作的值,也是没问题的,因为只要 Q 不选这个动作就可以
DDQN相对于原来的深度Q网络修改最少,几乎没有增加运算量。
竞争深度Q网络(dueling DQN)
相较于原来的 深度Q网络,它唯一的差别是改变了网络的架构
原来Q网络直接输出Q值,竞争深度Q网络不直接输出Q,而是分两条路径
第一条路经输出标量V(s),第二条输出向量A(s,a),加起来得到Q(s,a)
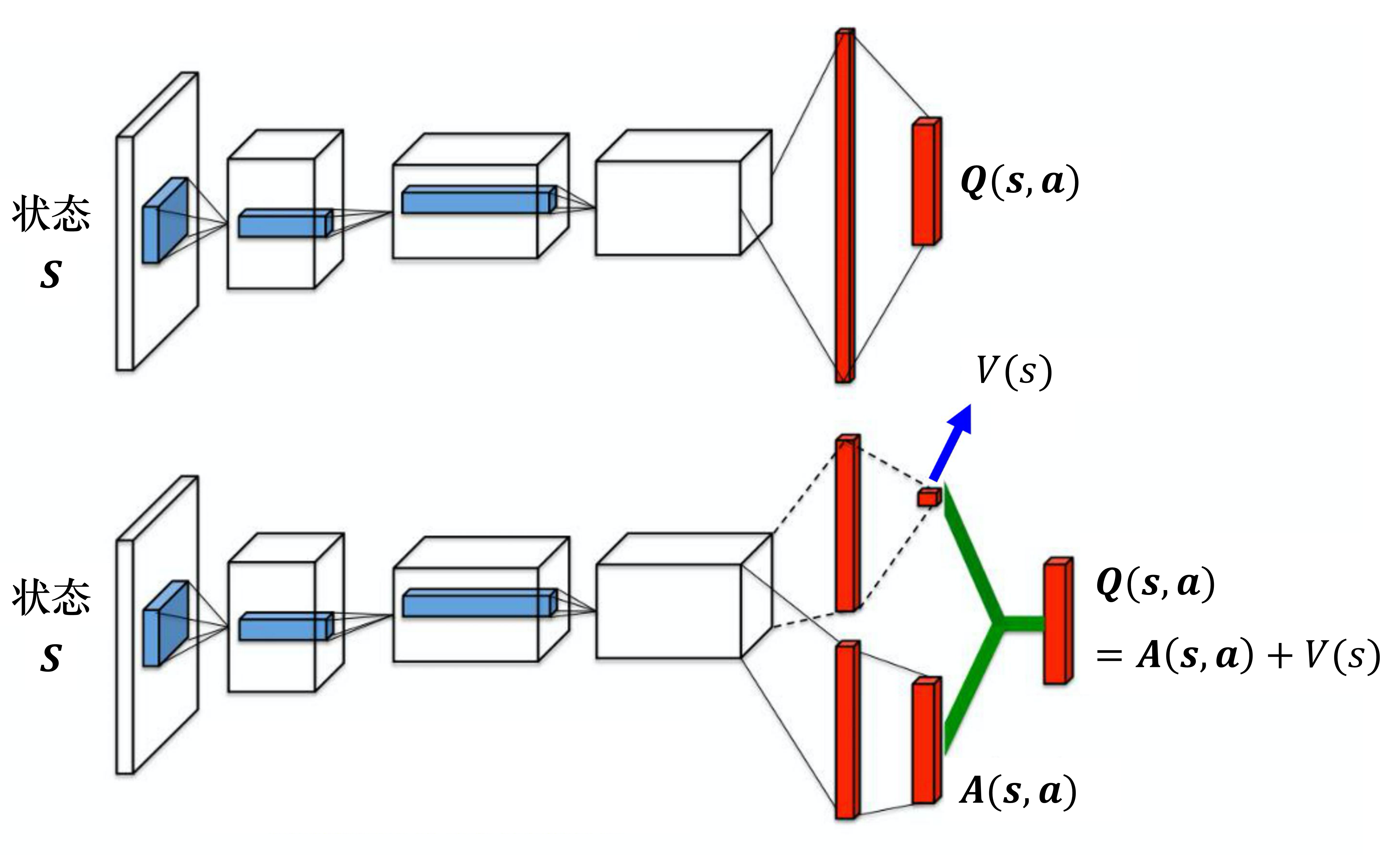
所以有可能我们在某一个状态下,只采样到这两个动作,没采样到第三个动作,但也可以更改第三个动作的 Q 值。这样的好处就是我们不需要把所有的状态-动作对都采样,可以用比较高效的方式去估计 Q 值。因为有时候我们更新的时候,不一定是更新Q表格,而是只更新了 V(s),但更新 V(s) 的时候,只要修改 V(s)的值,Q表格的值也会被修改。竞争深度Q网络是一个使用数据比较有效率的方法。
实际要给A一些约束,让A的更新比较麻烦,倾向于用V(s)解决问题。比如限制A的每一列和为0,所以A不能同时增加,就会强迫网络更新V
优先级经验回放(prioritized experience replay,PER)
假设有一些数据,我们之前采样过,发现这些数据的时序差分误差特别大(时序差分误差就是网络的输出与目标之间的差距),这代表我们在训练网络的时候,这些数据是比较不好训练的。既然比较不好训练,就应该给它们比较大的概率被采样到,即给它优先权(priority)。
在蒙特卡洛和时序差分方法中取地平衡
我们可以在蒙特卡洛方法和时序差分方法中取得平衡,这个方法也被称为多步方法
之前只采样了某一个步骤,所以得到的数据是真实的,接下来都是 Q 值估测出来的。现在采样比较多的步骤,采样 N 个步骤才估测值,所以估测的部分所造成的影响就会比较小。当然多步方法的坏处就与蒙特卡洛方法的坏处一样,因为 r 有比较多项,所以我们把 N 项的 r 加起来,方差就会比较大。但是我们可以调整 N 的值,在方差与不精确的 Q 值之间取得一个平衡。
噪声网络
ε-贪心这样的探索就是在动作的空间上加噪声,但是有一个更好的方法称为噪声网络(noisy net)
我们在网络的每一个参数上加上一个高斯噪声(Gaussian noise),就把原来的Q函数变成 Q~